Note: Because of changes in hosting by GeoGebra, the embedded exploration sketches are not currently functioning. Getting them working again is on my "To-Do" list!
Lunes and Triangles in Spherical Geometry
Stephen Szydlik
Department of Mathematics
University of Wisconsin Oshkosh
szydliks@uwosh.edu
Carol Seaman
Associate Professor Emerita
Department of Mathematics
The University of North Carolina at Greensboro
This is a worksheet for discovering some fascinating facts about lunes
and triangles on a sphere. Our first activity allows you to explore the
two-sided
polygon called a lune. Such polygons do not even exist in Euclidean
geometry! The sides of a lune are both half lines with common endpoints.
Recall that "lines" on a sphere are great circles. You can picture the
area of a lune as the area between two lines of longitude on a globe model
of the earth. The common endpoints of the sides of the lune are represented
by the north and south poles. In the figure below, the blue region
represents a lune. You may click and drag on the sphere to rotate it.

How Do We Find the Area of a Lune?
On the following disk model of the sphere, explore the relationship between the measure of the angles of the lune and its area. You may drag either point B or C in order to change the size of the lune. You will find questions to answer under the sketch.
Answer the following questions based on your findings:
- What is the relationship between the two angles of the lune? Why should this be happening?
- What is the relationship between the angle of the lune and the area of the lune and the area of the sphere? Can you explain how the area of a lune can be calculated if you know the angle of the lune?
- What is the relationship between the area of the lune ACDB and the area of the triangle ABC? Be specific! Why is it necessary to specify that the side CB goes through the center of the disk in order for this relationship to hold?
The Area of a Spherical Triangle Part 1:
How do we find area?
Now take a look at triangles on the sphere. Drag any vertex of triangle ABC and discover what happens to the angle sum and to the area of the triangle. Again, there will be questions to answer under the sketch.
Answer the following questions based on your findings:
- What do you notice about the angle sum of a spherical triangle? What is the smallest angle sum you were able to make? What is the largest?
- What is the relationship between the area of the triangle and the angle sum of the triangle?
- Can you find a way to calculate the area of the triangle if you know its angle sum?
The Area of a Spherical Triangle Part 2:
Making the Argument
Consider the following yellow spherical triangle. It is formed by the intersection of three lunes (green, blue, and red). (All three lunes include the yellow triangle.) Note that the triangle and also the lunes have associated "twins" antipodal to them, and these twins are given the same colors. Rotating the sphere by dragging it may help in visualizing the triangle and associated lunes.
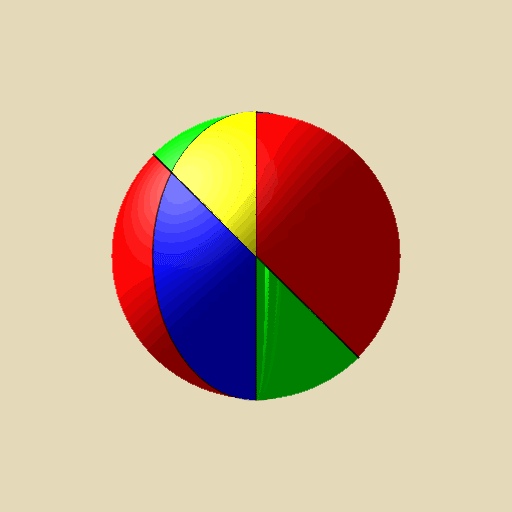
In the previous exercise, you explored the relationship between the angles of a spherical triangle and its area. Now it's time to make an argument why that works!
- Suppose you knew the (radian) measures of angles 1, 2, and 3. How would you find the area of the green lune? The blue lune? The red lune? (You might want to reload the page to reset the figure if you can't see the numbered angles.)
- If I add up the areas of the 3 lunes and their twins, do I get the (surface) area of the entire sphere? Why or why not?
- Write an equation relating the area of the lunes, the area of the triangle and the surface area of the sphere. Can you use this equation to develop a mathematical argument for your formula for the area of a triangle on the sphere?
Similar Triangles on the Sphere
Finally, take a look the question of whether or not two spherical triangles can be similar without being congruent. In the following sketch, drag the vertices of each triangle to try to form triangles with the same angle measures but with different areas.
What did you decide? Can similar but not congruent triangles exist on a sphere? Explain your answer based on your findings about the calculation of the area of a spherical triangle.
Comments on our exploration? Please email Stephen Szydlik at szydliks@uwosh.edu
