Math 301
Introduction to Probability and Statistics
Spring 2014
Section 001 9:10 to 10:10, M W F
Instructor:
Dr. Chris Edwards Phone: 424-1358 or 948-3969 Office: Swart 123
Classroom:
Swart 13 Text: Probability and
Statistics, 8th
edition, by Devore. Earlier editions of the text should be
acceptable.
Required
Calculator: TI-83, TI-83 Plus, or TI-84 Plus,
by Texas Instruments. Other TI
graphics calculators (like the TI-86) do not have the same statistics routines
we will be using and may cause you troubles. Link to
Day By Day notes here.
Catalog
Description: Elementary
probability models, discrete and continuous random variables, sampling and
sampling distributions, estimation, and hypothesis testing. Prerequisite: Mathematics 172 with a
grade of C or better.
Course
Objectives: The
goal of statistics is to gain understanding from data. This course focuses on critical thinking
and active learning. Students will
be engaged in statistical problem solving and will develop intuition concerning
data analysis, including the use of appropriate technology. Specifically
students will develop
¥ an
awareness of the nature and value of statistics
¥ a
sound, critical approach to interpreting statistics, including possible misuses
¥ facility
with statistical calculations and evaluations, using appropriate technology
¥ effective
written and oral communication skills
Grading:
Final grades are based on these 300 points:
|
|
Topic |
Points |
Tentative Date |
Chapters |
|
Exam 1 |
Summaries, Probability |
53 pts. |
March 10 |
1, 2, 3.1 to 3.3, 4.1 to 4.2 |
|
Exam 2 |
Distributions |
53 pts. |
April 18 |
3, 4, 5 |
|
Exam 3 |
Inference |
53 pts. |
May 16 |
7, 8 |
|
Group Presentations |
15 Points Each |
60 pts. |
Various |
|
|
Homework |
9 Points Each |
81 pts. |
Mostly Weekly |
|
Grades: Grades
will be assigned by the following schedule.
|
Grade |
Points (Percent) |
Grade |
Points (Percent) |
Grade |
Points (Percent) |
|
A |
270 (90 %) |
B- |
231 (77 %) |
D+ |
189 (63 %) |
|
A- |
261 (87 %) |
C+ |
219 (73 %) |
D |
180 (60 %) |
|
B+ |
249 (83 %) |
C |
210 (70 %) |
D- |
171 (57 %) |
|
B |
240 (80 %) |
C- |
201 (67 %) |
F |
170 or fewer |
Homework: I will collect three homework problems
approximately once a week. The due
dates are listed on the course outline below. While I will only be grading three
problems, I presume that you will be working on many more than just the three I
assign. I suggest that you work
together in small groups on the homework for this class. What I expect is a
well thought-out, complete discussion of the problem. Please donÕt just put down a numerical
answer; I want to see how you did
the problem. (You wonÕt get full
credit for just numerical answers.)
The method you use, and your description of your work, is much more
important to me than the final answer.
Presentations: There
will be four presentations, each worth 15 points. The descriptions of the presentations
are in the Day By Day Notes. I will
assign you to your groups for these presentations, because I want to avoid you having
the same members each time. I
expect each person in a group to contribute to the work; however, you can
allocate the work in any way you like.
If a group member is not contributing, see me as soon as possible so I
can make a decision about what to do.
The topics are: 1 –
Data Displays (February 21). 2
– Probability (March 7). 3
– Central Limit Theorem (April 25).
4 – Statistical Hypothesis Testing (May 14).
Office Hours: Office
hours are times when I will be in my office to help you. There are many other times when I am in
my office. If I am in and not busy,
I will be happy to help. My office
hours for Spring 2014 semester are 9:10 to 11:00 Tuesday, 3:00 to 4:00
Wednesday and Friday, or by appointment.
Philosophy: I
strongly believe that you, the student, are the only person who can make
yourself learn. Therefore, whenever
it is appropriate, I expect you to
discover the mathematics we will be exploring. I do not feel that lecturing to you will
teach you how to do mathematics. I hope
to be your guide while we learn some mathematics, but you will need to do the learning. I expect each of you to come to class
prepared to digest the dayÕs material.
That means you will benefit most by having read each section of the text
and the Day By Day notes before
class.
My idea of
education is that one learns by doing.
I believe that you must be engaged in the learning process to learn
well. Therefore, I view my job as a
teacher not as telling you the answers to the problems we will encounter, but
rather pointing you in a direction that will allow you to see the solutions
yourselves. To accomplish that
goal, I will find different interactive activities for us to work on. Your job is to use me, your text, your
friends, and any other resources to become adept at the material.
|
Monday |
Wednesday |
Friday |
|
February 3 Day 1 |
February 5 Day 2 |
February 7 Day 3 |
|
February 10 Day 4 |
February 12 Day 5 |
February 14 Day 6 |
|
February 17 Day 7 |
February 19 Day 8 |
February 21 Day 9 |
|
February 24 Day 10 |
February 26 Day 11 |
February 28 Day 12 |
|
March 3 Day 13 |
March 5 Day 14 |
March 7 Day 15 |
|
March 10 Day 16 |
March 12 Day 17 |
March 14 Day 18 |
|
March 17 Day 19 |
March 19 Day 20 |
March 21 Day 21 |
|
March 31 Day 22 |
April 2 Day 23 |
April 4 Day 24 |
|
April 7 Day 25 |
April 9 Day 26 |
April 11 Day 27 |
|
April 14 Day 28 |
April 16 Day 29 |
April 18 Day 30 |
April
21 Day 31 |
April 23 Day 32 |
April 25 Day 33 |
|
April 28 Day 34 |
April 30 Day 35 |
May 2 Day 36 |
|
May 5 Day 37 |
May 7 |
May 9 Day 39 |
|
May 12 Day 40 |
May 14 |
May 16 Day 42 |
Homework
Assignments: (subject to change if
we discover issues as we go)
Homework
1, due February 14
1) Anxiety
disorders and symptoms can often be effectively treated with medications. The accompanying data on a receptor
binding measure was read from a graph in a recent scientific paper on the
subject. Use various methods from Chapter 1 to describe and summarize the
data. In particular, we want to
highlight the differences between the two groups of patients.
PTSD: 10 20 25 28 31 35 37 38 38 39 39 42 46
Healthy: 23 39 40 41 43 47 51 58 63 66 67 69 72
2) Consider
a sample ![]() and
suppose that the values of
and
suppose that the values of ![]() and s have been calculated and are known. Let
and s have been calculated and are known. Let ![]() and
and ![]() for all iÕs. (The yÕs
have been ÒcenteredÓ and the zÕs have
been ÒstandardizedÓ.) Find the
means and standard deviations for the two new lists, y and z.
for all iÕs. (The yÕs
have been ÒcenteredÓ and the zÕs have
been ÒstandardizedÓ.) Find the
means and standard deviations for the two new lists, y and z.
3) Specimens
of three different types of rope wire were selected, and the fatigue limit was
determined for each specimen.
Construct a comparative box plot and a plot with all three quantile
plots superimposed. Comment on the
information each display contains.
Also explain which graphical display you prefer for comparing these data
sets. Keep in mind your goal is to
highlight the differences between the data sets.
Type
1 350 350 350 358 370 370 370 371 371 372 372 384 391 391 392
Type
2 350 354 359 363 365 368 369 371 373 374 376 380 383 388 392
Type
3 350 361 362 364 364 365 366 371 377 377 377 379 380 380 392
4) The
sample data ![]() sometimes
represents a time series, where
sometimes
represents a time series, where ![]() is the
observed value of a response variable x
at time t. Often the observed series shows a great
deal of random variation, which makes it difficult to study longer-term
behavior. In such situations, it is
desirable to produce a smoothed version of the series. One technique for doing so involves
exponential smoothing. A smoothing constant a
is chosen ( 0 < a
< 1) and then smoothed values
is the
observed value of a response variable x
at time t. Often the observed series shows a great
deal of random variation, which makes it difficult to study longer-term
behavior. In such situations, it is
desirable to produce a smoothed version of the series. One technique for doing so involves
exponential smoothing. A smoothing constant a
is chosen ( 0 < a
< 1) and then smoothed values ![]() are
calculated by
are
calculated by ![]() and for
and for ![]()
![]() .
.
a) Consider
the following time series of the temperature of effluent at a sewage treatment
plant on day t: 47, 54, 53, 50, 46,
46, 47, 50, 51, 50, 46, 52, 50, 50.
Plot each x against t.
Does there appear to be any pattern? Now calculate the ![]() Õs using a
= .1. Repeat for a = .5.
Which value of a
gives a smoother series?
Õs using a
= .1. Repeat for a = .5.
Which value of a
gives a smoother series?
b) Substitute
![]() on the
right-hand side of the expression for
on the
right-hand side of the expression for ![]() , then substitute
, then substitute ![]() in terms
of
in terms
of ![]() and
and ![]() , and so on.
On how many of the values
, and so on.
On how many of the values ![]() does
does ![]() depend?
What happens to the coefficient on
depend?
What happens to the coefficient on ![]() as k increases? If t
is large, how sensitive is
as k increases? If t
is large, how sensitive is ![]() to the
initial condition
to the
initial condition ![]() ?
?
Homework
2, due February 26
1) A
utility company offers a lifeline rate to any household whose electricity usage
falls below 240 kWh during a particular month. Let A
denote the event that a randomly selected household in a certain community does
not exceed the lifeline usage during January, and let B be the analogous event for the month of July (A and B refer to the same household). Suppose ![]() ,
, ![]() , and
, and ![]() . Compute a)
. Compute a) ![]() , and b) the probability that
the lifeline usage amount is exceeded in exactly one of the two months. Describe this last event in terms of A and B.
, and b) the probability that
the lifeline usage amount is exceeded in exactly one of the two months. Describe this last event in terms of A and B.
2) The
route used by a motorist to get to work has two stoplights. The probability of signal 1 being red is
.4 and for signal 2 it is .5. There
is a .6 probability that at least one of the two is red. What is the probability that both
signals are red? That the first is
red, but not the second? That exactly one signal is red?
3) Three
molecules of type A, three of type B, three of type C, and three of type D
are to be linked together to form a chain molecule. An example of one such chain molecule is
ABCDABCDABCD and another is BCDDAAABDBCC.
a) How many such
chain molecules are there? [Hint: If the three AÕs were distinguishable from one another, such as ![]() ,
, ![]() , and
, and ![]() , how many molecules would there
be? How is this number reduced when
the subscripts are removed from the AÕs?]
, how many molecules would there
be? How is this number reduced when
the subscripts are removed from the AÕs?]
b) Suppose a
chain molecule of the type described is randomly selected. What is the probability that all three
molecules of each type end up next to one another (such as in BBBAAADDDCCC)?
4) Three
married couples have purchased theater tickets and are seated in a row
consisting of just six seats. If
they take their seats in a completely random fashion (random order), what is
the probability that Jim and Paula (husband and wife) sit in the two seats on
the far left? What is the
probability that Jim and Paula end up sitting next to one another? What is the probability that at least
one of the wives ends up sitting next to her husband? [Note: you probably wonÕt be able to use
a formula to answer this; rather, a brute force listing of the sample space may
be a more fruitful strategy.]
Homework
3, due March 5
1) In
a Little League baseball game, suppose the pitcher has a 50 % chance of
throwing a strike and a 50 % chance of throwing a ball, and that successive pitches
are independent of one another.
Knowing this, the opposing team manager has instructed his hitters to
not swing at anything. What is the
chance that the batter walks on four pitches? What is the chance that the batter walks
on the sixth pitch? What is the
chance that the batter walks (not necessarily on four pitches)? Note: in baseball, if a batter gets
three strikes he is out, and if he gets four balls he walks.
2) A
car insurance company classifies each driver as good risk, medium risk, or poor
risk. Of their current customers,
30 % are good risks, 50 % are medium risks, and 20 % are poor risks. In any given year, the chance that a
driver will have at least one citation is 10 % for good risk drivers, 30 % for
medium risk drivers, and 50 % for poor risk drivers. If a randomly selected driver insured by
this company has at least one citation during the next year, what is the chance
that the driver was a good risk? A
medium risk?
3) An
insurance company offers its policyholders a number of different premium
payment options. For a randomly
selected policyholder, let X = the
number of months between successive payments. The cdf of X is:
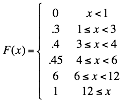
What is the pmf of X? Using just the cdf, compute P(3 ² X ² 6) and P(4 ² X).
[Of course you can use your pmf to check your work.]
4) The
pmf for X, the number of major
defects on a randomly selected appliance in our warehouse, is
![]()
Compute
E(X),
V(X)
using the definition, and V(X) using the shortcut.
Homework
4, due March 21
1) The
time it takes a read/write head to locate a desired record on a computer disk
once positioned on the right track can be reasonably modeled with a uniform
distribution. If the disk rotates
once every 25 msec, then assume ![]() . Compute P(10 ² X ² 20), P(10 ² X), the cdf F(X), E(X),
and V(X).
. Compute P(10 ² X ² 20), P(10 ² X), the cdf F(X), E(X),
and V(X).
2) Use
the following pdf and find a) the cdf b) the mean and c) the median of the
distribution.
![]() .
.
3) There
are two machines available for cutting corks intended for use in wine
bottles. The first produces corks
with diameters that are normally distributed with mean 3 cm and standard
deviation .1 cm. The second machine
produces corks with diameters that have a normal distribution with mean 3.04 cm
and standard deviation .02 cm.
Acceptable corks have diameters between 2.9 cm and 3.1 cm. Which machine is more likely to produce
an acceptable cork?
4) Suppose
the time it takes for Jed to mow his lawn can be modeled with a gamma
distribution using a = 2
and b
= 0.5. What is
the chance that it takes at most 1 hour for Jed to mow his lawn? At least 2 hours? Between 0.5 and 1.5 hours?
Homework
5, due April 4
1)
The data below are
precipitation values during March over a 30-year period in Minneapolis-St.
Paul.
0.77 1.20 3.00 1.62 2.81 2.48 1.74 0.47 3.09 1.31 1.87 0.96
0.81 1.43 1.51 0.32 1.18 1.89 1.20 3.37 2.10 0.59 1.35 0.90
1.95 2.20 0.52 0.81 4.75 2.05
Construct
and interpret a normal probability plot for this data set. The large outliers should make the data
look non-normal. Can a
transformation make the data more normal looking? Calculate the square root and the cube
root of each observation, and construct and interpret normal probability
plots. What do you conclude is the
best choice: leave the data along, use the square root, or use the cube root?
2) A
particular type of tennis racket comes in a midsize version and an oversize
version. Sixty percent of all
customers who shop at a certain store want the oversize version. Assume the next ten customers that come
to the store are a random sample of all customers. (This assumption is sometimes difficult
to justify in practice, but is almost always made to facilitate our
calculations. Whether this is good
practice or not is a worthy discussion.)
What is the chance that at least six of the next ten customers want the
oversize racket? What is the chance
that the number of customers out of the next ten who want the oversize racket
is within one standard deviation of the mean? If the store currently has only seven
rackets of each version, what is the chance that all of the next ten
customers can get the version they want?
[Hint: It might be easier to calculate the last part by examining the
complement.]
3) Suppose
n in a binomial experiment is known
and fixed. Are there any values of p for which the variance is zero? Explain this result in words. For what value of p is the variance maximized?
[Hint: Either graph variance as a function of p or try to minimize using calculus.]
Homework 6, due April 14
1) A
second stage smog alert has been called in a certain area of Los Angeles county
in which there are 50 industrial firms.
An inspector will visit 10 randomly selected firms to check for
violations of regulations. If 15 of
the firms are actually violating at least one regulation, what is the pmf of
the number of firms visited by the inspector that are in violation of at least
one regulation? Find the Expected
Value and Variance for your pmf.
2) A
couple wants to have exactly two girls and they will have children until they
have two girls. What is the chance
that they have x boys? What is the chance they have 4 children
altogether? How many children would
you expect this couple to have?
(Find the Expected Value.)
3) Let
X have a binomial distribution with n = 25. For p
= 0.5, 0.6, and 0.9, calculate the following probabilities both exactly and with the normal approximation to the
binomial. a) P(15 ² X ² 20). b) P(X ² 15). c) P(20
² X). Comment on the accuracy of the normal
approximation for these parameter choices.
Homework
7, due April 30
1) There
are 40 students in a statistics class, and from past experience, the instructor
knows that grading exams will take an average of 6 minutes, with a standard
deviation of 6 minutes. If grading
times are independent of one another, and the instructor begins grading at 5:50
p.m., what is the chance that grading will be done before the 10 p.m. news
begins?
2) A
student has a class that is supposed to end at 9:00 a.m. and another that is
supposed to begin at 9:10 a.m.
Suppose the actual ending time of the first class is normally
distributed with mean 9:02 and standard deviation 1.5 minutes. Suppose the starting time of the second
class is also normally distributed, with mean 9:10 and standard deviation 1
minute. Suppose also that the time
it takes to walk between the classes is a normally distributed random variable
with mean 6 minutes and standard deviation 1 minute. If we assume independence between all
three variables, what is the chance the student makes it to the second class
before the lecture begins? [Hint:
Consider the quantity ![]() . Positive values of
. Positive values of ![]() correspond to making it to class on
time.]
correspond to making it to class on
time.]
3) A
90 % confidence interval for the true average IQ of a group of 100 people is
(114.4, 115.6). Deduce the sample
mean and population standard deviation used to calculate this interval, and
then produce a 99 % interval from the same data.
4) An
experimenter would like to construct a 99% confidence interval with a length of
no more than 0.2 ohms, for the average resistance of a segment of copper cable
of a certain length. If the
experimenter is willing to assume that the true standard deviation is no larger
than 0.15 ohms, what sample size would you recommend?
Homework
8, due May 7
1) Fifteen
samples of soil were tested for the presence of a compound, yielding these data
values: 26.7, 25.8, 24.0, 24.9,
26.4, 25.9, 24.4, 21.7, 24.1, 25.9, 27.3, 26.9, 27.3, 24.8, 23.6. Is it plausible that these data came
from a normal curve? Support your
answer. Now calculate a 95%
confidence interval for the true average amount of compound present. Comment on any assumptions you had to
make.
2) A
hot tub manufacturer advertises that with its heating equipment, a temperature
of 100¡F can be achieved in at most 15 minutes. A random sample of 32 tubs is selected,
and the time necessary to achieve 100¡F is determined for each tub. The sample average time and sample
standard deviation are 17.5 minutes and 2.2 minutes, respectively. Does this data cast doubt on the
companyÕs claim? Calculate a
P-value, and comment on any assumptions you had to make.
3) A
sample of 50 lenses used in eyeglasses yields a sample mean thickness of 3.05
mm and a population standard deviation of .30 mm. The desired true average thickness of
such lenses is 3.20 mm. Does the
data strongly suggest that the true average thickness of such lenses is
undesirable? Use a
= .05. Now suppose the experimenter
wished the probability of a Type II error to be .05 when m
= 3.00. Was a sample of size 50
unnecessarily large?
4) Suppose
that the true average viscosity should be 3000 in a certain process. Do the following measurements support
that standard? State and test the
appropriate hypotheses.
2781 2900 3013 2856 2888
Homework
9, due May 12
1) A
random-number generator is supposed to produce a sequence of 0s and 1s with
each value being equally likely to be a 0 or a 1 and with all values being
independent. In an examination of
the random-number generator, a sequence of 50,000 values is obtained of which
25,264 are 0s.
a) Formulate
a set of hypotheses to test whether there is any evidence that the
random-number generator is producing 0s and 1s with unequal probabilities, and
calculate the corresponding P-value.
b) Compute
a 99% confidence interval for the probability p that a value produced by the random-number generator is a 0.
c) If a
two-sided 99% confidence interval for this probability is required with a total
length no larger than 0.005, how many additional values need to be
investigated?
2) In
a survey of 4,722 American youngsters, 15 % were seriously overweight, as
measured by BMI. Calculate and
interpret a 99 % confidence interval for the proportion of all American
youngsters who are seriously overweight.
Discuss whether the Associated Press (who reported this data) actually
took or could have taken a random sample of American youngsters.
3) In
is known that roughly 2/3 of all human beings have a dominant right foot or
eye. Is there also right-sided
dominance in kissing behavior? One
scientific article reported that in a random sample of 124 kissing couples,
both people in 80 of the couple tended to lean more to the right than to the
left. If 2/3 of all kissing couples
exhibit this right-leaning behavior, what is the probability that the number in
a sample of 124 who do so differs from the expected value by at least as much
as what was actually observed? (i.e.
calculate a P-value.) Does the
result of the experiment suggest that the 2/3 figure is plausible or
implausible? State and test the
appropriate hypotheses.
Managed
by: chris
edwards
Last
updated January 14, 2014