MATH 201 Applied Statistics

Spring 2014

Section 006 10:20 to 11:20 M W F

Section 004 1:50 to 2:50 M W F

Instructor: Dr. Chris Edwards Phone: 424-1358 or 948-3969 Office: Swart 123

Classroom: Swart 127 Text: Introduction to the Practice of Statistics 7^th edition, by David S. Moore and George P. McCabe. Earlier editions of the text will likely be adequate, but you will have to allow for different page references. Link to Day By Day notes here.

Required Calculator: TI-83, TI-83 Plus, or TI-84 Plus, by Texas Instruments. Other TI graphics calculators (like the TI-86) do not have the same statistics routines we will be using and will cause you troubles.

Catalog Description: An introduction to applied statistics using a statistical computing package such as MINITAB. Topics include: Descriptive statistics, elementary probability, discrete and continuous distributions, interval and point estimation, hypothesis testing, regression and correlation. Prerequisite: Mathematics 104 or 108 with a grade of C or better.

Course Objectives: (Click here for full document.) The goal of statistics is to gain understanding from data. This course focuses on critical thinking and active learning. Students will be engaged in statistical problem solving and will develop intuition concerning data analysis, including the use of appropriate technology.

Specifically students will develop

• an interest and aptitude in applying statistics to other areas of human inquiry

• an awareness of the nature and value of statistics

• a sound, critical approach to interpreting statistics, including possible misuses

• facility with statistical calculations and evaluations, using appropriate technology

• effective written and oral communication skills

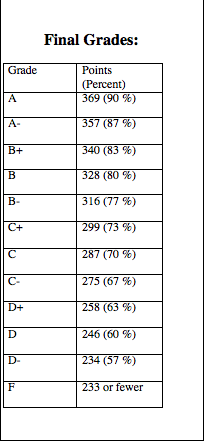
Grading: Final grades are based on 410 points:

	Topic	Points	Tentative Date
Exam 1	Descriptive Statistics	93 pts.	March 7
Exam 2	Sampling, Probability, and the CLT	93 pts.	April 16
Exam 3	Statistical Inference	83 pts.	May 16
Group Presentations	20 Points Each	60 pts.	Biweekly
Homework	9 Points Each	81 pts.	Weekly

Attendance is a very important component of success in my class because many of the skills and lessons we will learn will be a direct result of classroom activities that cannot be reproduced easily. Please attend class as often as you can. You are responsible for any material you miss. The Day By Day notes will help you greatly in this regard.

Presentations: There will be three presentations, each worth 20 points. The descriptions of the presentations are in the Day By Day Notes. I will assign you to your groups for these presentations, as I want to avoid you having the same members each time. I expect each person in a group to contribute to the work; you can allocate the work in any way you like. If a group member is not contributing, see me as soon as possible so I can make a decision about what to do. Part of your presentation grade will be based on your own evaluations of how each person contributed to the presentation. The topics are: 1 – Displays and Regression (March 5). 2 – Sampling and Probability (April 14). 3 – Statistical Hypothesis Testing (May 14).

Homework: I will collect several homework problems approximately once a week. The due dates are listed on the course outline below. While I will only be grading a few problems, I presume that you will be working on many more than just the ones I assign. I suggest that you work together in small groups on the homework for this class. What I expect is a well thought-out, complete discussion of the problem. Please don’t just put down a numerical answer; I want to see how you did the problem. (You won’t get full credit for just numerical answers.) The method you use and your description is much more important to me than the final numerical answer. Important Grading Feature: If your homework percentage is lower than your exam percentage, I will replace your homework percentage with your exam percentage. Therefore, your homework percentage cannot be lower than your exam percentage.

Office Hours: Office hours are times when I will be in my office to help you. There are many other times when I am in my office. If I am in and not busy, I will be happy to help. My office hours for Spring 2014 semester are 9:10 to 11:00 Tuesday, 3:00 to 4:00 Wednesday and Friday, or by appointment.

Philosophy: I strongly believe that you, the student, are the only person who can make yourself learn. Therefore, whenever it is appropriate, I expect you to discover the mathematics we will be exploring. I do not feel that lecturing to you will teach you how to do mathematics. I hope to be your guide while we learn some mathematics, but you will need to do the learning. I expect each of you to come to class prepared to digest the day’s material. That means you will benefit most by having read each section of the text and the Day By Day notes before class.

My idea of education is that one learns by doing. I believe that you must be engaged in the learning process to learn well. Therefore, I view my job as a teacher not as telling you the answers to the problems we will encounter, but rather pointing you in a direction that will allow you to see the solutions yourselves. To accomplish that goal, I will find different interactive activities for us to work on. Your job is to use me, your text, your friends, and any other resources to become adept at the material.

Homework Assignments: (subject to change if we discover issues as we go)

Homework 1, due February 14

1) The formal name for garbage is “municipal solid waste.” Here is a breakdown of the materials that made up American municipal solid waste:

Material	Weight (million tons)	Percent of total (%)
Food scraps	31.7	12.5
Glass	13.6	5.3
Metals	20.8	8.2
Paper, paperboard	83.0	32.7
Plastics	30.7	12.1
Rubber, leather, textiles	19.4	7.6
Wood	14.2	5.6
Yard trimmings	32.6	12.8
Other	8.2	3.2
Total	254.1	100.0

(Note: The totals do not add precisely due to individual round-off errors.)

Made a bar graph of the percentages. The graph gives a clearer picture of the main contributors to garbage if you order the bars from tallest to shortest. Label your graph, and use a ruler (or software) to make it look professional.

Also make a pie chart of the percentages, either by hand or using software. Notice that is it easier to see small differences (as in Food scraps, Plastics, and Yard trimmings) with the bar graph rather than the pie chart. (Observe that any categorical list can be converted to percentages, and therefore to a pie chart.)

Comment on which display you prefer for summarizing categorical information.

2) People with diabetes must monitor and control blood glucose level. The goal is to maintain “fasting plasma glucose” between about 90 and 130 mg/dl. Here are the fasting plasma glucose levels for 18 diabetics enrolled in a diabetes control class (five months after the end of the class) and for 16 diabetics who were given individual instruction on diabetes control.

Class Instruction Group

141 158 112 153 134 95 96 78 148 172 200
271 103 172 359 145 147 255

Individual Instruction Group

128 195 188 159 227 198 163 164 159 128 283
226 223 221 220 160

Make a back-to-back stem plot to compare the class and individual instruction groups. (You will want to trim and also split stems. Remember to include a definition of your stem unit.) How do the distribution shapes compare? Which group did better at keeping their glucose levels in the desired range?

3) In 1798 the English scientist Henry Cavendish measured the density of the Earth by careful work with a torsion balance. The variable recorded was the density of the Earth as a multiple of the density of water. Here are Cavendish’s 29 measurements.

5.50 5.61 4.88 5.07 5.26 5.55 5.36 5.29 5.58 5.65 5.57
5.53 5.62 5.29 5.44 5.34 5.79 5.10 5.27 5.39 5.42 5.47
5.63 5.34 5.46 5.30 5.75 5.68 5.85

Present these measurements graphically using either a stem plot, a histogram, or a quantile plot, and explain the reason for your choice. Then briefly discuss the main features of the distribution. In particular, what is your estimate (a single number) of the density of the Earth based on these measurements?

Homework 2, due February 21

1) The Wade Tract in Thomas County, Georgia, is an old-growth forest of longleaf pine trees (Pinus palustris) that has survived in a relatively undisturbed state since before the settlement of the area by Europeans. A study collected data for 584 of these trees. One of the variables measured was the diameter at breast height (DBH). This is the diameter of the tree (in cm) at 4.5 feet above the ground. Here are the diameters of a random sample of 40 trees with DBH greater than 1.5 cm.

10.5 13.3 26.0 18.3 52.2 9.2 26.1 17.6 40.5 31.8 47.2
11.4 2.7 69.3 44.4 16.9 35.7 5.4 44.2 2.2 4.3 7.8
38.1 2.2 11.4 51.5 4.9 39.7 32.6 51.8 43.6 2.3 44.6
31.5 40.3 22.3 43.3 37.5 29.1 27.9

Find the five-number summary for these data and the associated box plot. (As usual, label appropriately.) Also make a histogram and a quantile plot, and compare the three displays, noting similarities and differences.

2) Different varieties of the tropical flower Heliconia are fertilized by different species of hummingbirds. Over time, the lengths of the flowers and the form of the hummingbirds’ beaks have evolved to match each other. Here are data on the lengths in mm of three varieties of these flowers on the island of Dominica:

H. bihai

47.12 46.75 46.81 47.12 46.67 47.43 46.44 46.64 48.07 48.34 48.15
50.26 50.12 46.34 46.94 48.36

H. caribaea red

41.90 42.01 41.93 43.09 41.47 41.69 39.78 40.57 39.63 42.18 40.66
37.87 39.16 37.40 38.20 38.07 38.10 37.97 38.79 38.23 38.87 37.78
38.01

H. caribaea yellow

36.78 37.02 36.52 36.11 36.03 35.45 38.13 37.10 35.17 36.82 36.66
35.68 36.03 34.57 34.63

Make box plots to compare the three distributions. (Use the same scale for each plot, to make appropriate comparisons.) Report the five-number summaries along with your graph. What are the most important differences among the three varieties of flower?

3) High-density lipoprotein (HDL) is sometimes called the “good cholesterol” because low values are associated with a higher risk of heart disease. According to the American Heart Association, people over the age of 20 years should have at least 40 mg/dl of HDL cholesterol. US women aged 20 and over have a mean HDL of 55 mg/dl with a standard deviation of 15.5 mg/dl. Assume that the distribution is Normal.

a) HDL levels of 40 mg/dl or lower are considered low. What percent of women have low values of HDL?

b) HDL levels of 60 mg/dl or higher are believed to protect people from heart disease. What percent of women have protective levels of HDL?

c) HDL levels between 40 and 60 mg/dl are considered intermediate, neither very good nor very bad. What percent of women are in this category?

Homework 3, due February 28

1) How strong is the relationship between the score of the first exam and the score on the final exam in an elementary statistics course? Here are data for eight students from such a course:

First exam score 153 144 162 149 127 118 158 153
Final exam score 145 140 145 170 145 175 170 160

Which variable should play the role of explanatory variable in describing this relationship? Make a scatter plot and describe the relationship in words. Give some possible reasons why this relationship is not strongly linear.

2) Each of the following statements contains a blunder. Explain in each case what is wrong.

a) “There is a high correlation between the age of American workers and their occupation.”

b) “We found a high correlation (r = 1.19) between students’ ratings of faculty teaching and ratings made by other faculty members.”

c) “The correlation between the gender of a group of students and the color of their cell phone was r = 0.23.”

3) The New York City Open Accessible Space Information System Cooperative (OASIS) is an organization of public and private sector representatives that has developed an information system designed to enhance the stewardship of open space. Data from the OASIS Web site for 12 large US cities follow. The variables are population (in thousands) and open total park or open space within city limits (in acres).

City	Population (in thousands)	Open Acreage
Baltimore	651	5,091
Boston	589	4,865
Chicago	2,896	11,645
Long Beach	462	2,887
Los Angeles	3,695	29,801
Miami	362	1,329
Minneapolis	383	5,694
New York	8,008	49,854
Oakland	399	3,712
Philadelphia	1,518	10,685
San Francisco	777	5,916
Washington, D.C.	572	7,504

Make a scatter plot of the data using population as the explanatory variable and open space as the response variable. Is it reasonable to fit a straight line to these data, for either explanatory or predictive purposes? Explain why or why not. Report the least squares regression equation and superimpose the line on your graph. Include the value for r-squared.

Homework 4, due March 17

1) Explain what is wrong with each of the following randomization procedures and describe how you would do the randomization correctly.

a) Twenty students are to be used to evaluate a new treatment. Ten men are assigned to receive the treatment and ten women are assigned to be the controls.

b) Ten subjects are to be assigned to two treatments, five to each. For each subject, a coin is tossed. If the coin comes up heads, the subject is assigned to the first treatment; otherwise they are assigned to the second treatment.

c) An experiment will assign forty rats to four different treatment conditions. The rats arrive from the supplier in batches of ten, and the treatment lasts two weeks. The first batch of ten rats is randomly assigned to one of the four treatments, and data for these rats are collected. After a one-week break, another batch of ten rats arrives and is assigned randomly to one of the three remaining treatments. The process continues until the last batch of rats is given the treatment that has not been assigned to the three previous batches. (For purposes of correctly randomizing, assume that you cannot control the fact that there will be four shipments of ten rats each.)

2) Systematic random samples are often used to choose a sample of apartments in a large building or dwelling units in a block at the last stage of a multistage sample. An example will help illustrate the idea of a systematic sample. Suppose that we must choose four addresses out of 100. Because 100/4 = 25, we can think of the list as four lists of 25 addresses. Choose one of the first 25 at random, using your calculator. The sample contains this address and the addresses 25, 50, and 75 places down the list from it. If ‘13’ is chosen, for example, then the systematic random sample consists of the addresses numbered 13, 38, 63, and 88.

A study of dating among college students wanted a sample of 200 of the 9,000 single male students on campus. The sample consisted of every 45^th name from a list of the 9,000 male students. Explain why the survey chooses every 45^th name. Using your calculator, choose the starting point for this systematic sample. Be sure to indicate clearly which calculator command(s) you used.

3) An opinion poll in California uses random digit dialing to choose telephone numbers at random. Numbers are selected separately within each California area code. The size of the sample in each area code is proportional to the population living there. What is the name for this kind of sampling design? California area codes, in rough order from north to south are

530 707 916 209 415 925 510 650 408 831 805 559
760 661 818 213 626 323 562 709 310 949 909 858
619

Another California survey does not call numbers in all area codes, but starts with an SRS of ten area codes. Using your calculator, choose such an SRS. Be sure to indicate clearly which calculator command(s) you used.

Homework 5, due April 2

1) All human blood can be “ABO-typed” as one of O, A, B, or AB, but the distribution of the types varies a bit among groups of people. Here are the distributions for the US and Ireland:

Blood type	A	B	AB	O
US	0.42	0.11	0.03	0.44
Ireland	0.35	0.10	0.03	0.52

Choose a person at random from each country, independently from one another. What is the probability that both people have type O blood? What is the probability that both have the same blood type? (A chart like the one we made for rolling two dice will help here, but note that the events are not equally likely.)

2) Internet sites often vanish or move, so that references to them can’t be followed. In fact, 13% of Internet sites referenced in papers in major scientific journals are lost within two years after publication. If a paper contains seven Internet references, what is the probability that all seven are still good two years later? What specific assumptions did you make in order to calculate this probability? (A probability tree may help understand this calculation, but the problem can be completed without using a tree.)

3) Non-standard dice can produce interesting distributions of outcomes. You have two balanced, six-sided dice. One is a standard die, with faces having 1, 2, 3, 4, 5, and 6 spots. The other die has three faces with 1 spot, 2 faces with 4 spots, and one face with 10 spots. Find the probability distribution for the total number of spots on the up-faces when you roll these two dice. (A chart like the one we made for rolling two standard dice will help here, but note that the events are not equally likely for the second die.)

Homework 6, due April 9

1) Role-playing games like Dungeons & Dragons use many different types of dice. Suppose that a four-sided die has faces marked 1, 2, 3, and 4. To determine the intelligence of your character, you roll this die twice, and add 1 to the resulting sum of the spots. We assume the faces are equally likely and the two rolls are independent. What is the average intelligence for such characters? How spread out are their intelligences, as measured by the standard deviation of the distribution?

2) Eighty percent of women at a certain university enroll in the education program, while twenty percent of men do. Twenty-five percent of the students are females at this school. What percentage of education majors are women? What percentage of non-education majors are men?

3) The scores of high school seniors on the ACT college entrance examination in a recent year had a mean of 19.2 and a standard deviation of 5.1. The distribution of scores is not exactly Normal (ACT score is clearly not a continuous variable) but the Normal curve is a close approximation. (I will show an example in class.)

a) What is the approximate probability that a single student, randomly chosen from all those taking the test, scores 23 or higher?

b) What is the approximate probability that the mean of 25 randomly chosen students from among all those taking the test is 23 or higher?

c) Which of the two calculations above is more accurate? (Note that part a is really a question from Chapter 1 material.)

Homework 7, due April 28

1) To assess the accuracy of a laboratory scale, a standard weight known to weight exactly 10 grams is weighed repeatedly. The scale readings are Normally distributed with unknown mean (this mean is 10 grams if the scale has no bias, however). The standard deviation of the scale readings is known (from years of use) to be 0.0002 grams. The weight is measured five times, with a mean value of 10.0023 grams. Give a 95% confidence interval for the mean of repeated measurements of the weight. (Note that the calculator only allows room for 5 digits and a decimal, making this interval’s upper and lower values the same. To conquer this shortcoming of the calculator, consider measuring in “milligrams above 10”.)

How many measurements would have to be taken to get a margin of error of ±0.0001 with 95% confidence?

2) State the appropriate null hypothesis and alternative hypothesis in each of the following cases. Make sure you mention a parameter in your answer.

a) A 2008 study reported that 88% of students owned a cell phone. You plan to take an SRS of college students to see if the percentage has increased.

b) The examinations in a large freshman chemistry class are scaled after grading so that the mean score is 75. The professor thinks that students who attend early morning recitation sections will have a higher mean score than the class as a whole. Her students this semester can be considered a sample from the population of all student she might teach, so she compares their mean score with 75.

c) The student newspaper at your college recently changed the format of their opinion page. You take a random sample of students and select those who regularly read the newspaper. They are asked to indicate their opinions on the changes using a five-point scale: -2 if the new format is much worse than the old, -1 if the new format is somewhat worse than the old, 0 if the new format is about the same as the old, +1 if the new format is somewhat better than the old, and +2 if the new format is much better than the old.

3) One way to measure whether the trees in the Wade Tract are uniformly distributed is to examine the average location in the north-south or the east-west direction. The values range from 0 to 200, so if the trees are uniformly distributed, the average location should be 100, and any differences in the actual sample would be due to random chance. The actual sample mean in the north-south direction for the 584 trees in the tract is 99.74. A theoretical calculation for uniform distributions (the details are beyond the scope of this course) gives a standard deviation of 58. Carefully state the null and alternative hypotheses in terms of the true average north-south location. Test your hypotheses by reporting your results along with a short summary of your conclusions.

Homework 8, due May 5

1) An agronomist examines the cellulose content of a variety of alfalfa hay. Suppose that the cellulose content in the population has a standard deviation of 8 mg/g. A sample of 15 cuttings has mean cellulose content of 145 mg/g.

a) Give a 90% confidence interval for the true population mean cellulose content.

b) A previous study claimed that the mean cellulose content was 140 mg/g, but the agronomist has reason to believe that the mean is higher than that figure. State the hypotheses and carry out a significance test to see if the new data support this belief.

c) What assumptions do you need to make for these statistical procedures to be valid?

2) Facebook provides a variety of statistics on their Web site that detail the growth and popularity of the site. One such statistic is that the average user has 130 friends. Consider the following data, the number of friends in a SRS of thirty Facebook users from a large university.

99 148 158 126 118 112 103 111 154 85 120
127 137 74 85 104 106 72 119 160 83 110
97 193 96 152 105 119 171 128

a) Do you think these data come from a Normal distribution? Use a graphical summary to help make your explanation.

b) Explain why it is or is not appropriate to use the t-procedures to compute a 95% confidence interval for the true mean number of friends for Facebook users at this large university.

c) Find the 95% confidence interval for the true mean number of friends for Facebook users at this large university.

3) If we increase our food intake, we generally gain weight. Nutrition scientists can calculate the amount of weight gain that would be associated with a given increase in calories. In one study, sixteen non-obese adults, aged 25 to 36 years, were fed 1,000 calories per day in excess of the calories needed to maintain a stable body weight. The subjects maintained this diet for 8 weeks, so they consumed a total of 56,000 extra calories. According to theory, 3,500 extra calories will translate into a weight gain of one pound. Therefore, we expect each of these subjects to gain 56,000/3,500 = 16 pounds. Here are the weights before and after the 8-week period, expressed in kg.

Subject	1	2	3	4	5	6	7	8
Weight before:	55.7	54.9	59.6	62.3	74.2	75.6	70.7	53.3
Weight after:	61.7	58.8	66.0	66.2	79.0	82.3	74.3	59.3
Subject	9	10	11	12	13	14	15	16
Weight before:	73.3	63.4	68.1	73.7	91.7	55.9	61.7	57.8
Weight after:	79.1	66.0	73.4	76.9	93.1	63.0	68.2	60.3

a) For each subject, find the weight gain (or loss) by subtracting the weight before from the weight after.

b) Convert the 16 pounds expectation to kg by dividing by the conversion factor of 2.2. Now state the null and alternative hypotheses for this matched pairs test.

c) Conduct the test and state your conclusions. Include a P-value in your summary.

Homework 9, due May 12

1) Corporate advertising tries to enhance the image of the corporation. A study compared two ads from two sources, the Wall Street Journal and the National Enquirer. Subjects were asked to pretend that their company was considering a major investment in Performax, the fictitious sportswear firm in the ads. Each subject was asked to respond to the question, “How trustworthy was the source in the sportswear company ad for Performax?” on a 7-point scale. Higher values indicated more trustworthiness. Here is a summary of the data:

Ad source	Sample size	Mean	Standard Deviation
Wall Street Journal	66	4.77	1.50
National Enquirer	61	2.43	1.64

Compare the two sources using a t-test and state your conclusions. Include a P-value in your summary. Also include a 95% confidence interval for the true difference in the trustworthiness for these two sources.

2) The Pew Research Center recently polled 1,048 US drivers and found that 69% enjoyed driving their automobiles.

a) Construct a 95% confidence interval for the true proportion of US drivers who enjoy driving their automobiles.

b) In 1991, a Gallup Poll reported this percent to be 79%. Does the Pew data indicate that the percentage now is different from the 79% figure reported by Gallup? Perform a z-test and state your conclusions, including a P-value in your summary.

3) A Pew Internet Project Data Memo presented data comparing adult gamers with teen gamers with respect to the devices on which they play. The data are from two surveys. The adult survey had 1,063 games while the teen survey had 1,064 gamers. The memo reports that 54% of adult gamers played on game consoles (Xbox, PlayStation, Wii, etc.) while 89% of teen gamers played on game consoles. Test the null hypothesis that the two proportions are equal and state your conclusions, including a P-value in your summary.

Monday	Wednesday	Friday
February 3 Day 1 Introduction	February 5 Day 2 Graphical Summaries Section 1.1	February 7 Day 3 Arizona Temps Section 1.1
Feburary 10 Day 4 Numerical Summaries Section 1.2	February 12 Day 5 Standard Deviation Section 1.2	February 14 Day 6 Homework 1 Due Intro to Normal Section 1.3
February 17 Day 7 Normal Problems Section 1.3	February 19 Day 8 Correlation Sections 2.1 and 2.2	February 21 Day 9 Homework 2 Due Outliers I Section 2.2
February 24 Day 10 Olympic Races Section 2.3	February 26 Day 11 Outliers II Section 2.3	February 28 Day 12 Homework 3 Due U. S. Population Sections 2.4 and 2.5
March 3 Day 13 Polls Section 3.1 to 3.3	March 5 Day 14 Presentation 1 Review	March 7 Day 15 Exam 1
March 10 Day 16 Lurking Variables Section 3.1	March 12 Day 17 SRS’s Section 3.2	March 14 Day 18 Sampling Schemes Sections 3.3 and 3.4
March 17 Day 19 Homework 4 Due Randomness Section 4.1	March 19 Day 20 Coins, Dice, RV’s Section 4.2	March 21 Day 21 Random Variables Section 4.3
March 31 Day 22 Means and Variances Section 4.4	April 2 Day 23 Homework 5 Due Trees and Bayes’ Section 4.5	April 4 Day 24 Binomial Section 5.2
April 7 Day 25 Central Limit Theorem Section 5.1	April 9 Day26 Homework 6 Due More CLT Section 5.1	April 11 Day 27 Review
April 14 Day 28 Presentation 2	April 16 Day 29 Exam 2	April 18 Day 30 m&m’s Section 6.1

April 21 Day 31 CI Practice Section 6.1	April 23 Day 32 Contradiction Section 6.2	April 25 Day 33 Hypothesis Test Practice Section 6.2
April 28 Day 34 Homework 7 Due Testing Simulation Section 6.2 to 6.3	April 30 Day 35 Gosset Simulation Section 7.1	May 2 Day 36 Matched Pairs Section 7.1
May 5 Day 37 Homework 8 Due Two Samples Section 7.2	May 7 Day 38 Proportions Section 8.1	May 9 Day 39 2 Sample Proportions Section 8.2
May 12 Day 40 Homework 9 Due Review	May 14 Day 41 Presentation 3 Review	May 16 Day 42 Exam 3

Return to Chris’ Homepage

Return to UW Oshkosh Homepage

Managed by chris edwards
Last updated January 14, 2014